av Ahmad E för 4 årar sedan
395
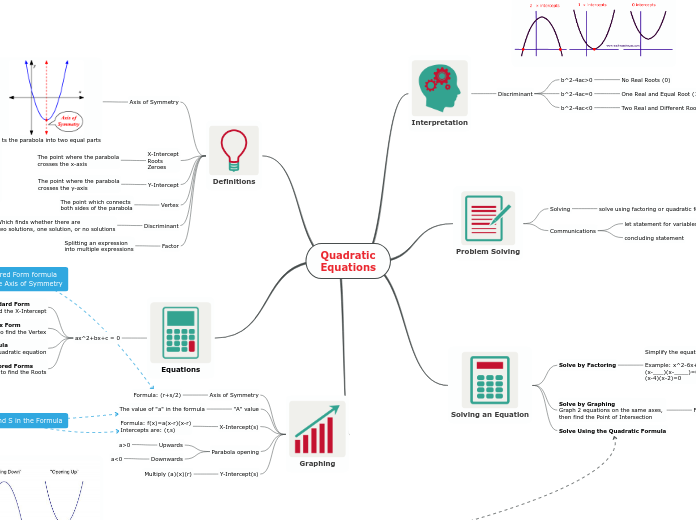
Quadratic Equations
Quadratic equations are fundamental in algebra and involve expressions where the highest exponent of the variable is two. These equations are typically written in the form ax² + bx + c = 0.
av Ahmad E för 4 årar sedan
395

Mer av detta
a<0
a>0
f(x) = a(x-r )(x-r )
(-b±√b^2-4ac) / 2a
Vertex y = a(x – h)^2 + k
y=ax^2+bx+c
1) solve for x 2) plug the value of x into the original equation to find y
Zero Product Property When equation has product of two simple equations, one of the two (or both) must be equal to zero
1) Factor 2) Find the 2 Solutions 3) Solve each Equation
Example: (x-4)(x-2) (x-4)=0 because x=4 and/or (x-2)=0 because x=2
Two Real and Different Roots (3)
One Real and Equal Root (1)
No Real Roots (0)