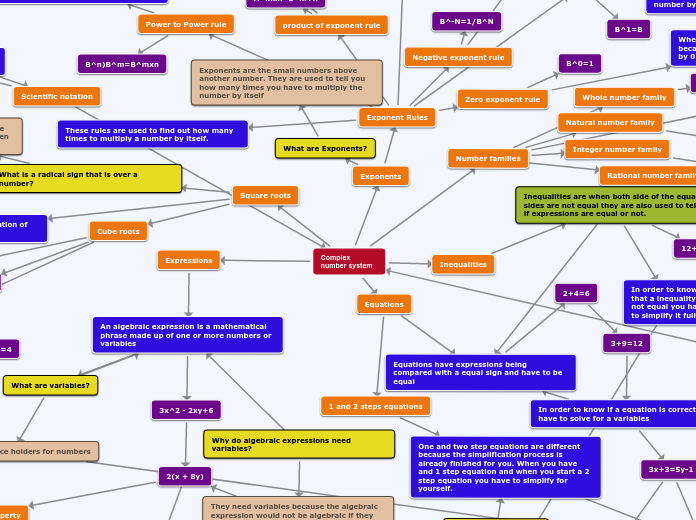
The text focuses on solving linear relations and equations, including the process of isolating variables and rearranging formulas. It outlines methods for handling equations involving fractions and multi-step operations, emphasizing the importance of performing inverse operations in the correct sequence.
calculate the slope, M, of the line using the two points (2,4) and (8,7)
+6 (8,7) +3 (2,4)
the total cost for an ice cream sundae with different numbers of toppings. if X represents the number of toppings and Y represents the total cost in dollars
graph a line using the y-intercept and the slope
= 2
1
slope = rise
run
the y-intercept is -3, so plot (0,-3) first. in y = mx + b form, the slope of the line is the coefficient of X, which is 2
y = 2x -3
identify the slope and y-intercept
Identify the slope and the y-intercept of a linear relation involving temperature
The slope of F = 1.8c +32 and F - intercept is +32
the rate of change in the y-values is consistently + 1.8 and when X = 0, Y = 32
the relationship between temperatures in degrees Fahrenheit and degrees Celsius is linear. the equation can be written. y = 1.8x + 32. X is in degrees Celsius and Y is in degrees Fahrenheit 0*c converts to +32*F
the slope of the line is 1.8 and the vertical intercept is +32
F = 1.8c + 32
for the linear relation identify the slope and the y-intercept
Operation's with fractions
and Decimals
= 4/3
= 16 divided 4
12 divided 4
16/12
Operation's with integer's
= 13
= 5 + 8
5 - (-8)
Common factors
greatest whole number that divides
evenly into both 18 and 21 is 3
factors of 21: 1,3,7 and 21
factors of 18: 1,2,16,9 and 18
18,21
Working with Variables
x = -2
-3x/-3 = 6/-3
-3x = 6
Key terms
run
Rise
y-intercept
Coefficient
Rate Of Change
Slope
Linear Relation
Key Terms
Formula Variable Term
Opposite Operations
Constant Term
Standard Form
Solve A Linear Equation Involving a fraction
k = 12
0.75k = 9
0.75 0.75
0.75k = 9
3k = 9
4
Working With Fractions
the least number that appears in both is 12. 12 is the least common denominator
6: 6,12,24,30,36
4: 4,12,16,20,24
list the multiple's of each denominator
denominator is the least common multiple of the denominations.
denominator is the least common multiple
1/4, 5/6 ( the least common)
rearrange formulas
y - b = mx
m m
y - b = x
m
divide both sides of the equation by m to isolate x
y - b = mx
y = mx + b, solve for X
y = mx + b subtract b from both sides of the equation
y - b = mx + b - b
Evaluating Expressions
5
8 - 3
4 (2) + 3 (-1)
4x + 3y
Evaluate each expression for x = 2 and y = -1
identify the steps required to solve a multi-step liner equation
or to solve the equation, perform the opposite operations in revers orders
the solution is
X = 25
divide by 2 to find the value of X
50 = 25
2
subtract 10 from the product
60 - 10 = 50
multiply 20 by 3
20 x 3 = 60
2x + 10 = 20
3
divide by 3
the result = 20
multiply x by 2
add 10 to the product
Volume of a gas
810 = 5x
5 5
162 = x
start with
725
subtract
455
multiply by
3
divide by
5
result is
162
810 = 5x
270 = 5x
3
3(270) = 3
(5x/3)
start with
X
multiply by
5
Divide by
3
add
455
result is
725
725 = 5x + 455
3
725 - 455 = 5x + 455 - 455
3
y = mx + b
volume of has is 725 cm3
between the volume of a gas in cubic centimeters Y and the temperature in degrees Celsius X
Simplifying Algebraic Expressions
= 2+7r + 4z
= 4 - 2 + 4r +3r - z + 5z
4 + 4r - z + 3r + 5z - 2
Solve a two - step linear equation
X = 2
2x = 4
remove zero pairs
2x - 3 + 3 = 1 + 3
to keep the equation balanced, add 3 to the right side
to isolate the variable term, 2x add 3 to the left side
