arabera Christopher Voss 12 years ago
359
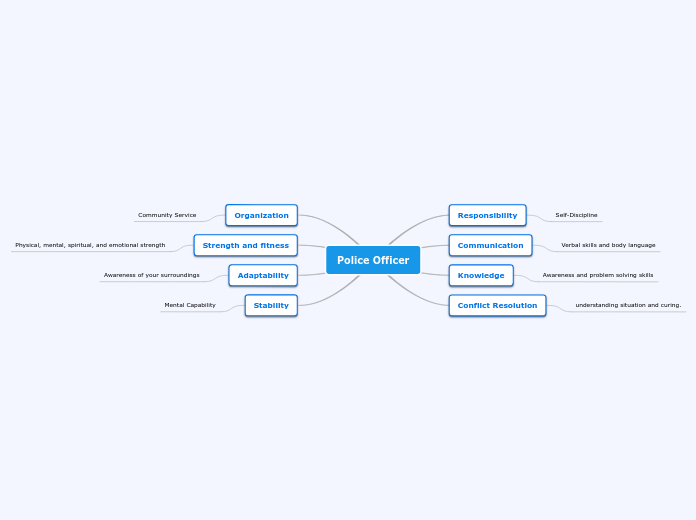
Diff EQ
The discussion focuses on various aspects of differential equations, including their existence, uniqueness, and methods for solving them. It covers both first-order and higher-order differential equations, examining linear homogeneous and nonhomogeneous types, and explores techniques such as the LaPlace Transform, separation of variables, and integrating factors.