NÚMEROS RACIONALES Y SU PRESENTACIÓN

Honelako gehiago

CLASE_MEDIADIADA POR TIC

by Jose Luis Peña Vergara

LOS NUMEROS REALES

by Manuel Ome Mosquera

MATEMÁTICA BÁSICA

by evelyn valencia cañaveral

Números decimales

by Gricelda Sanchez

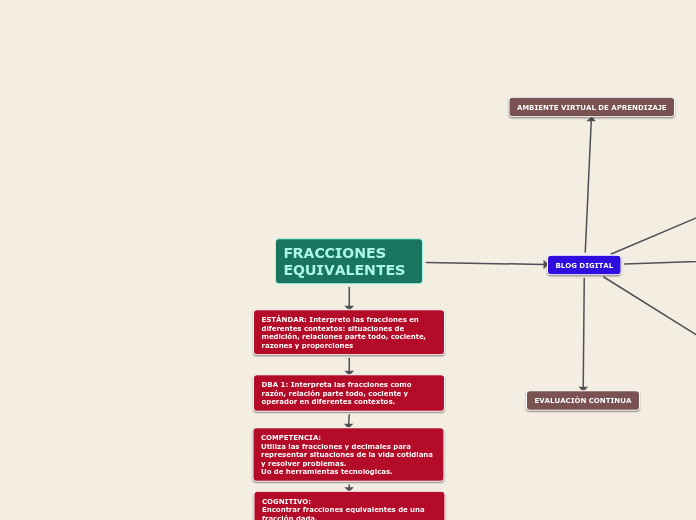
NÚMEROS RACIONALES Y SU PRESENTACIÓN

OPERACIONES CON FRACCIONES

SUMAS Y RESTAS: Si no tienen el mismo denominador, se saca el máximo común divisor (MCD) del denominador y se procede como el anterior.

7/12+ 9/20+3/4=(35+27+45)/60=107/60

PRODUCTOS DE FRACCIONES: Se multiplican los numeradores y denominadores, de ser posible se pueden simplificar el resultado.

7/2*4/3* 5/4=140/24=35/6

COCIENTES DE FRACCIONES: Se multiplican la primera por el inverso de la segunda fracción, de ser posible se pueden simplificar el resultado.

12/5÷4/25 =12/5*25/4=300/20=15/1=15

TIPOS DE FRACCIONES

FRACCIONES EQUIVALENTES

Dos fracciones son equivalentes si tienen el mismo valor numérico.

16/4=4; 21/3=7; 50/2=25

FRACCIONES IRREDUCTIBLES

Son todas aquellas fracciones cuyo numerador y denominador tienen como divisor común a la unidad.

14/13; 15/4; 17/31

FRACCIONES REDUCTIBLES

Cuando el numerador y denominador poseen algún divisor distinto de uno.

40/16; 81/27; 110/2

FRACCIONES HETEROGÉNEAS

Dos o más fracciones son heterogéneas si sus denominadores son diferentes.

41/17; 9/4; 13/3

FRACCIONES HOMOGÉNEAS

Dos o más fracciones son homogéneas si sus denominadores son iguales.

7/7; 9/7; 12/7

Los números racionales son aquellos que pueden ser expresados como una fracción. la letra que identifica al conjunto de los números racionales es la "Q". es decir a/b ; b ≠ 0, donde a representa el numerador y el b el denominador distinto de cero.

REPRESENTACIÓN DE NÚMEROS RACIONALES EN LA RESTA NUMÉRICA

7/2 -5/2 3/2 -1/2 -4 -3 (-5)/2 -2 -1 (-1)/2 0 1 3/2 2 3 7/2 4

A las distintas fracciones se las puede representar como decimales o viceversa. Los números racionales pueden ser expresados:

PERIÓDICO MIXTO

Son los números decimales en cuya parte decimal hay una parte periódica y otra no periódica

5/6=0,8333…=0,83 ̂

PERIÓDICO PURO

La parte decimal se repite periódicamente

4/3=1,333…=1,⏞3

EXACTO

La parte decimal tiene un número finito de cifras

EJEMPLO

1/4=0,25 ; 3/6=0,5