jonka Pablo Jimenez 4 vuotta sitten
1729
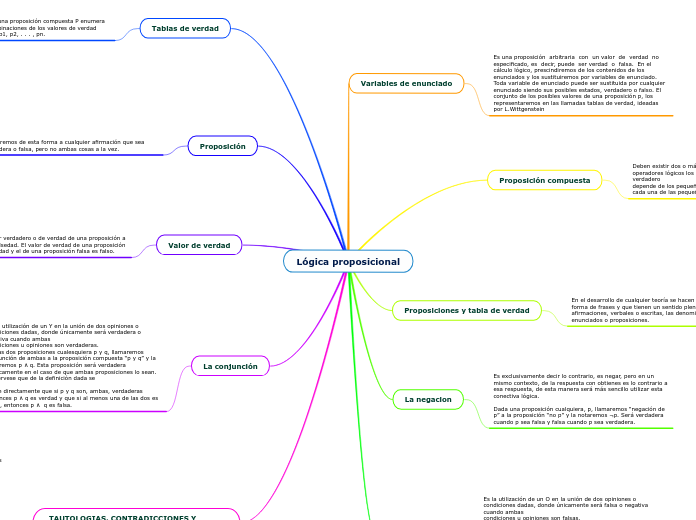
Lógica proposicional
La lógica proposicional se enfoca en el análisis y uso de proposiciones compuestas, las cuales se forman mediante la combinación de proposiciones simples con operadores lógicos como '
jonka Pablo Jimenez 4 vuotta sitten
1729

Lisää tämän kaltaisia