jonka rafaeel rehman 7 vuotta sitten
234
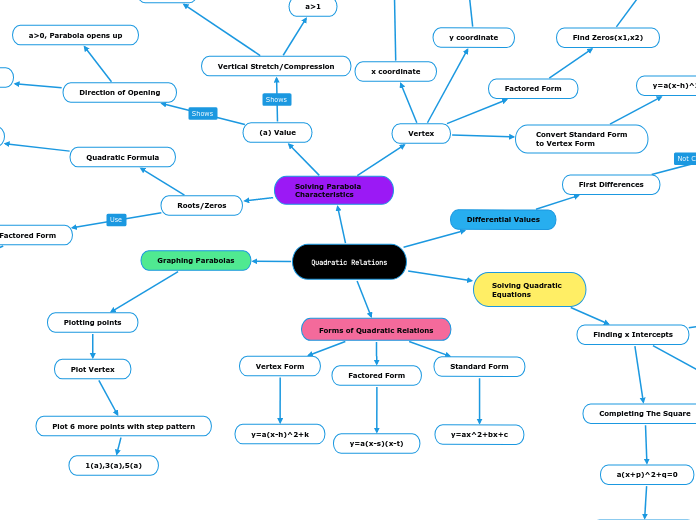
Quadratic Relations
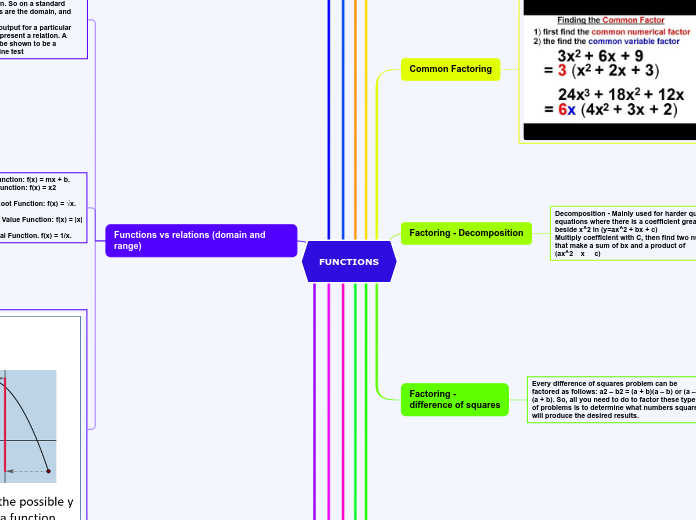
The text discusses various methods for working with quadratic expressions, including expanding, factoring, and using the distributive property. It explains how to expand expressions by squaring binomials and applying the FOIL method.