Quadratic Relations

Mais informações

Advanced Functions CPT

por Shana Van Elderen

Quadratics Concept Map Assignment

por Rushikesh Amin

Quadratic Equations

por Ahmad E

Sources of Finance

por nurul farah khairul azman

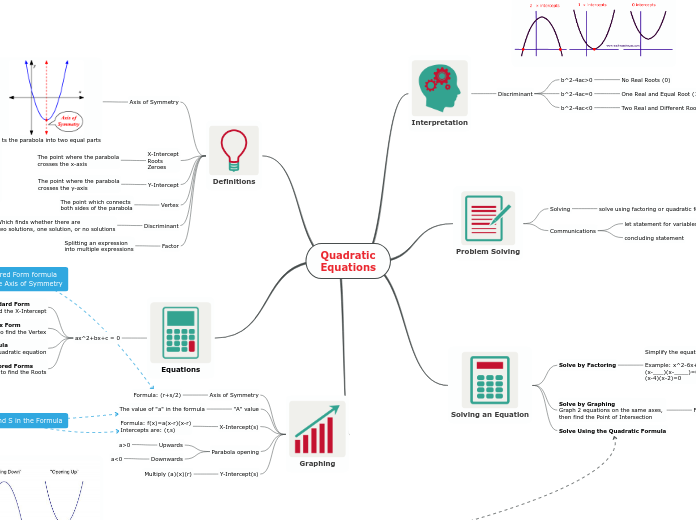
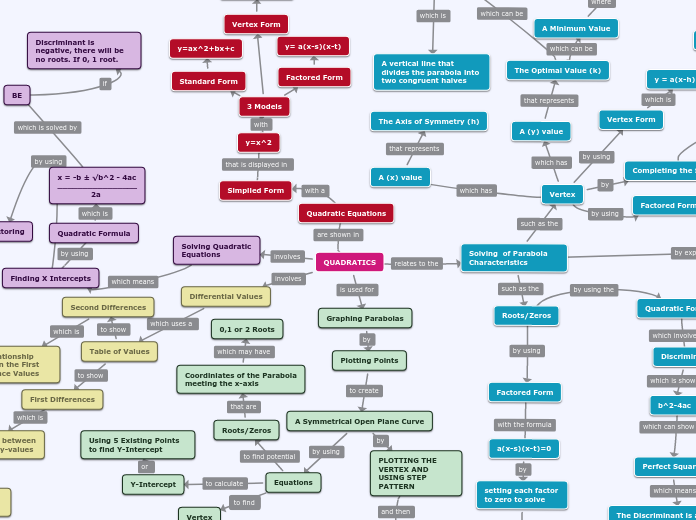
Quadratic Expressions

Expanding

Difference of squares

Follow FOIL method and remember to cancel out reciprocals.

(a-b)(a+b) =A^2+ab-ab+B^2 =A^2+B^2

Squaring binomials

Expand, then follow foil method.

(a+b)^2 =(a+b)(a+b) =a^2+2ab+b^2

Multiplying Binomials

Follow FOIL method.

(2x+4)(3x+2) =6x^2+12x+6

Distributive property

Multiply everything inside the brackets by the number(s) outside of it.

3(2x+4) =6x+12

Factoring

Difference of Squares

square root both terms and have a square outside the bracket to show it was factored, expand both terms, and follow binomial common factor.

36y^2-100 =(6y)^2-(10)^2 =(6y)(6y)-(10)(10) =(6y-10)(6y+10)

Perfect Square Trinomials

A^2-2AB+B^2 =(A-B)(A-B)

A^2+2AB+B^2 =(A+B)(A+B)

A=/=1

ax+bx+c

_ * _=ac

_+_=b

A=1

(1)x^2+bx+c =(x+1)(x+c)

Group Common Factors

Group both sides so to factor them separately

X^4-2x^3 + 4x-8

Binomial Common Factors

x-3 is multiplied by both 2 and 3y, making it able to factor out.

2(x-3)+3y(x-3) =(x-3)(2+3y)

Monomial Common Factors

Both x and y are being multiplied by 3, making it able to be factored out.

3y+3x =3(x+y)