jonka Sanchez Martínez Yael Ahuitz 2 vuotta sitten
175
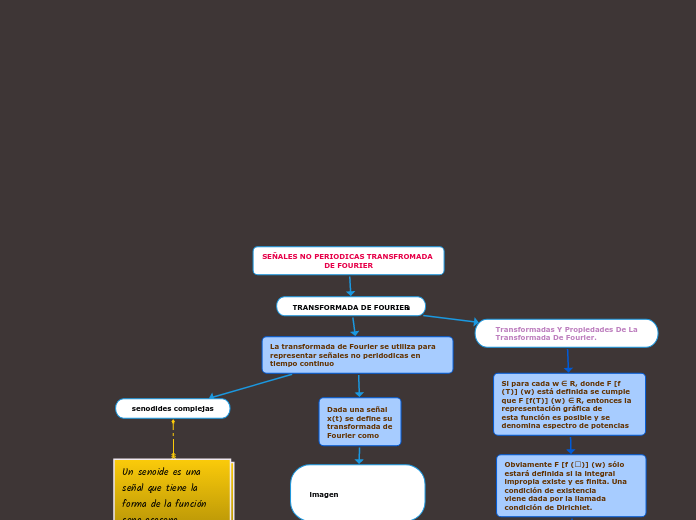
SEÑALES NO PERIODICAS TRANSFROMADA DE FOURIER
La transformada de Fourier es una herramienta fundamental en el análisis de señales, especialmente para aquellas que no son periódicas en el tiempo continuo. Para que la transformada de Fourier de una señal x(