a Kristina Semyonova 4 éve
374
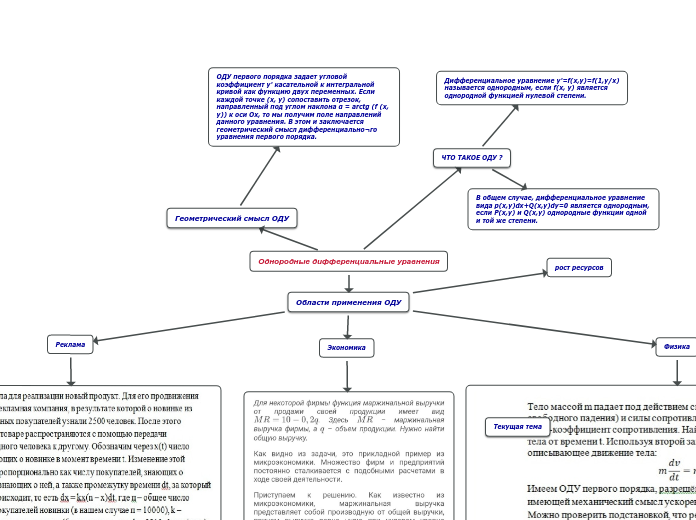
Однородные дифференциальные уравнения
Однородные дифференциальные уравнения (ОДУ) первого порядка важны для понимания углового коэффициента касательной к интегральной кривой, представляя собой функцию двух переменных. Геометрический смысл ОДУ заключается в создании поля направлений, где каждой точке на плоскости соответствует отрезок с углом наклона, определяемым функцией.