da JOHANA MADROÑERO mancano 2 anni
234
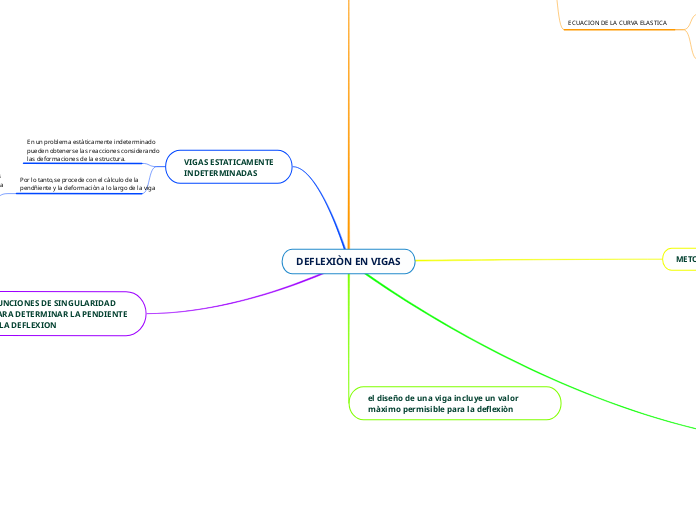
DEFLEXIÒN EN VIGAS
El análisis de la deflexión en vigas prismáticas puede abordarse eficazmente mediante el método de integración, que permite calcular la pendiente y la deflexión siempre que el momento flector se represente con una función analítica.