DISTRIBUCIÓN BINOMIAL Y DISTRIBUCIÓN NORMAL

Più simili a questo

PRECIOS Y MARGENES EN EL CANAL DE DISTRIBUCION

da Ivan Calvo

MICRORELATO

da Martín Llano

MEDIDAS DE DISTRIBUCION

da HERBERT MORENO

ANÁLISIS CASO ZARA

da DANIELA CAROLINA ESTRELLA NARVAEZ

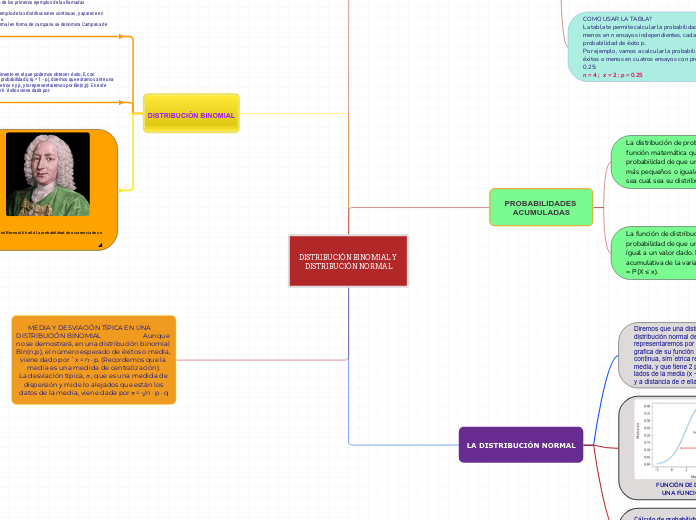
DISTRIBUCIÓN BINOMIAL Y DISTRIBUCIÓN NORMAL

LA DISTRIBUCIÓN NORMAL

Cálculo de probabilidades en normales Propiedad: Si X sigue una distribución N(x; σ) , entonces la variable Z = X − x σ sigue una distribución N(0,1). (El paso de la variable X −→ N(x; σ) a la Z −→ N(0;1) se denomina tipificación de la variable X).

FUNCIÓN DE DENSIDAD DE UNA FUNCIÓN NORMAL

Diremos que una distribución de probabilidad sigue una distribución normal de media x y desviación tíıpica σ, y lo representaremos por N(x; σ) cuando la representación grafica de su función de densidad es una curva positiva continua, sim´etrica respecto a la media, de m´aximo en la media, y que tiene 2 puntos de inflexión , situados a ambos lados de la media (x − σ y x + σ respectivamente) y a distancia de σ ella, es decir de la forma.

PROBABILIDADES ACUMULADAS

La función de distribución acumulativa especifica la probabilidad de que una variable aleatoria sea menor o igual a un valor dado. La función de distribución acumulativa de la variable aleatoria X es la función F(x) = P(X ≤ x).

Función de distribución acumulada

La distribución de probabilidad acumulada es una función matemática que se emplea para saber la probabilidad de que una variable aleatoria tome valores más pequeños o iguales que un número en concreto, sea cual sea su distribución.

Añada su texto

USO DE LAS TABLAS DE DISTRIBUCION BINOMIAL

COMO USAR LA TABLA? La tabla te permite calcular la probabilidad de obtener x éxitos o menos en n ensayos independientes, cada uno con una probabilidad de éxito p. Por ejemplo, vamos a calcular la probabilidad de obtener dos éxitos o menos en cuatros ensayos con probabilidad de éxito de 0.25: n = 4 ; x = 2 ; p = 0.25

La probabilidad que buscamos es 0.9492.

Para usar las tablas de la distribución binomial es necesario conocer: El número de veces que se realiza el experimento (n). La probabilidad de éxito (p). El número de éxitos (k). La probabilidad p se busca en la primera fila (valores desde 0’01 hasta 0’5). El número de veces que se realiza el experimento, en la primera columna (valores desde 2 a 10) y el número de éxitos a su lado

EJEMPLO DE USO DE TABLA BINOMIAL

MEDIA Y DESVIACIÓN TÍPICA EN UNA DISTRIBUCIÓN BINOMIAL Aunque no se demostrará, en una distribución binomial Bin(n;p), el número esperado de éxitos o media, viene dado por ¯x = n · p. (Recordemos que la media es una medida de centralización). La desviación típica, σ , que es una medida de dispersión y mide lo alejados que están los datos de la media, viene dada por σ = √n · p · q

DISTRIBUCIÒN BINOMIAL

Daniel Bernoulli halló la probabilidad de ocurrencia de un suceso aun siendo imposible contar los casos favorables: lo que no se puede hallar a priori se puede obtener a posteriori, mediante la observación múltiple de resultados de pruebas similares

Si realizamos n veces un experimento en el que podemos obtener éxito, E, con probabilidad p y fracaso, F, con probabilidad q (q = 1 − p), diremos que estamos ante una distribución binomial de parámetros n y p, y lo representaremos por Bin(n;p). En este caso la probabilidad de obtener k ´éxitos viene dada por:

Función de probabilidad de la distribución binomial, también denominada función de la distribución de Bernoulli,

La distribución binomial es uno de los primeros ejemplos de las llamadas distribuciones discretas . La distribución normal es un ejemplo de las distribuciones continuas, y aparece en multitud de fenómenos sociales. La grafica de la distribución normal en forma de campana se denomina Campana de Gauss.

Campana de Gauss