Coefficiente binomiale
(n) : (k+1)esimo valore (n+1)esima riga
(k) Tartaglia
(n) = (n)
(k) (n-k)
(n) = (n) = n
(1) (n-1)
(n) = (n) = 1
(0) (n)
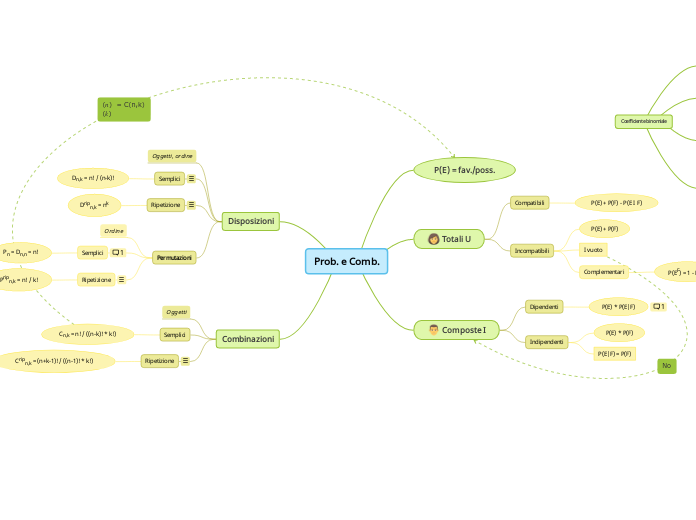
Prob. e Comb.
Combinazioni
COMBINAZIONI di n oggetti a k a k dove ciascun elemento al massimo k volte
Cripn,k = (n+k-1)! / ((n-1)! * k!)
Cn,k = n! / ((n-k)! * k!)
Oggetti
Disposizioni
Permutazioni
permutazioni di n oggetti di cui k uguali
Pripn,k = n! / k!
oggetti sempre quelli, cambia solo ordine
Pn = Dn,n = n!
Ordine
Ripetizione
DISPOSIZIONI di n oggetti a k a k dove ciascun elemento figura al massimo k volte
Dripn,k = nk
Semplici
n oggetti presi k alla volta (a k a k)
Dn,k = n! / (n-k)!
Oggetti, ordine
Composte I
Indipendenti
P(E|F) = P(F)
P(E) * P(F)
Dipendenti
P(E) * P(E|F)
O contrario
Totali U
Incompatibili
Complementari
P(EF) = 1 - P(F)
I vuoto
P(E) + P(F)
Compatibili
P(E) + P(F) - P(E I F)
P(E) = fav./poss.