Площади фигур
Выпуклый четырехугольник
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p - a)(p - b)(p - c)(p - d)
Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p - a)(p - b)(p - c)(p - d) - abcd cos^2θ
S - площадь четырехугольника,
a, b, c, d - длины сторон четырехугольника,
p = (a + b + c + d)/2 - полупериметр четырехугольника,
θ = (α + β)/2 - полусумма двух противоположных углов четырехугольника.
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними
S = 1/2 d1 d2 sin α
Четырехугольник
Трапеция
S - площадь трапеции,
a, b - длины основ трапеции,
c, d - длины боковых сторон трапеции,
p =(a + b + c + d)/2- полупериметр трапеции.
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высоту
S = 1/2 (a + b) · h
Формула Герона для трапеции
S =(a + b)/|a - b| √(p-a)(p-b)(p-a-c)(p-a-d)
Параллелограм
S - Площадь параллелограмма,
a, b - длины сторон параллелограмма,
h - длина высоты параллелограмма,
d1, d2 - длины диагоналей параллелограмма,
α - угол между сторонами параллелограмма,
γ - угол между диагоналями параллелограмма
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
S = 1/2d1d2 sin γ
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
S = a · b · sin α
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
Ромб
S - Площадь ромба,
a - длина стороны ромба,
h - длина высоты ромба,
α - угол между сторонами ромба,
d1, d2 - длины диагоналей
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
S = 1/2(d1 · d2)
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
S = a^2 · sin α
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
S = a · h
Прямоугольник
S - Площадь прямоугольника,
a, b - длины сторон прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон
S = a · b
Квадрат
S - площадь квадрата,
a - длина стороны квадрата,
d - длина диагонали квадрата
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
S = 1/2d^2
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
S = a^2
Круг
S - Площадь круга,
r - длина радиуса круга,
d - длина диаметра круга
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.
S = 1/4πd^2
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.
S = πr^2
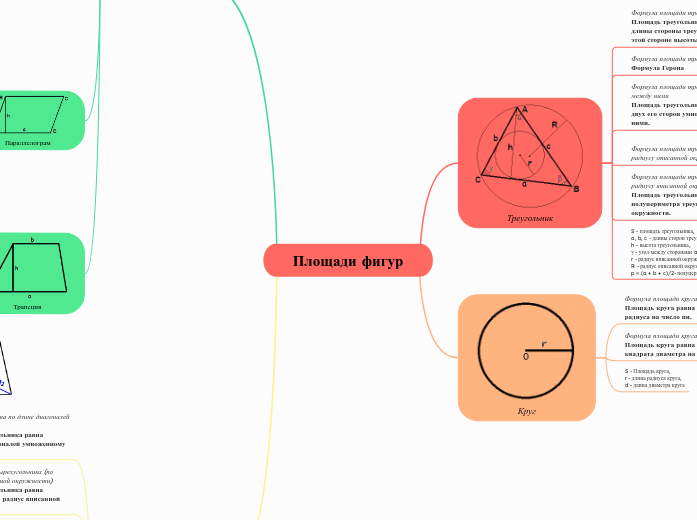
Треугольник
S - площадь треугольника,
a, b, c - длины сторон треугольника,
h - высота треугольника,
γ - угол между сторонами a и b,
r - радиус вписанной окружности,
R - радиус описанной окружности,
p = (a + b + c)/2- полупериметр треугольника.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
S = p · r
Формула площади треугольника по трем сторонам и радиусу описанной окружности
S = (a · b · с)
/4R
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 1/2 (a · b · sin γ)
S = 1/2 (a · c · sin β)
S = 1/2 (b · c · sin α)
Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p - a)(p - b)(p - c)
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
S = 1/2 (a · h)