by Noel martinez 7 years ago
311
Programación
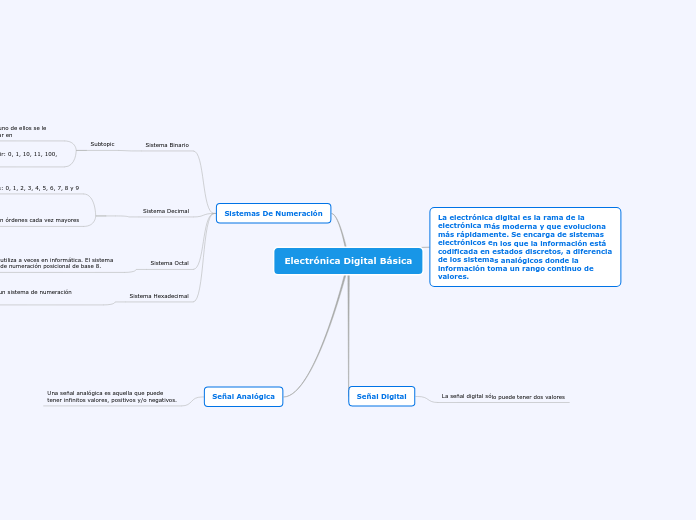
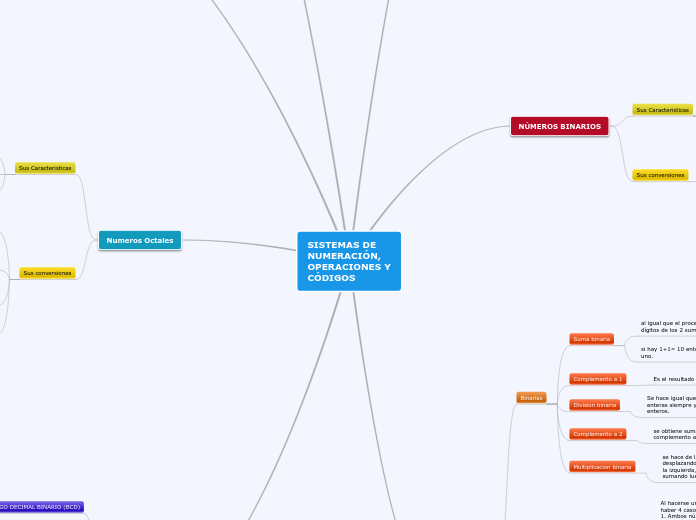
Un sistema de numeración es un conjunto estructurado de símbolos y reglas que permiten representar datos numéricos. Existen varios tipos de sistemas de numeración, cada uno con diferentes bases y símbolos.