av DANIEL SHANG 3 år siden
207
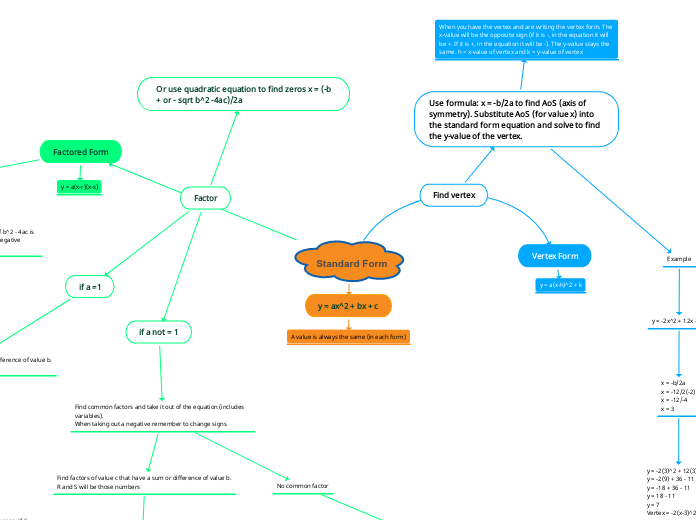
Standard Form
The process of finding the vertex of a quadratic function involves using the formula x = -b/2a to determine the axis of symmetry (AoS). Once you have the AoS, substitute this value back into the standard form equation to find the y-value of the vertex.