Standard Form

Mais informações

Favorite Number Project

por Isaac Ludgate

Chapter 4,5,6: Quadratic Relations

por Patel Sheil

Lucky numbers

por Isaiah Francis - Springbrook PS (1445)

Tree Organigram

por Sarah Howell

Special occasions

When the two factors are the same number there is only 1 x-int

y = x^2 + 10x + 25 25 = 5x5 5+5 = 10 y = (x+5)(x+5) y = (x+5)^2

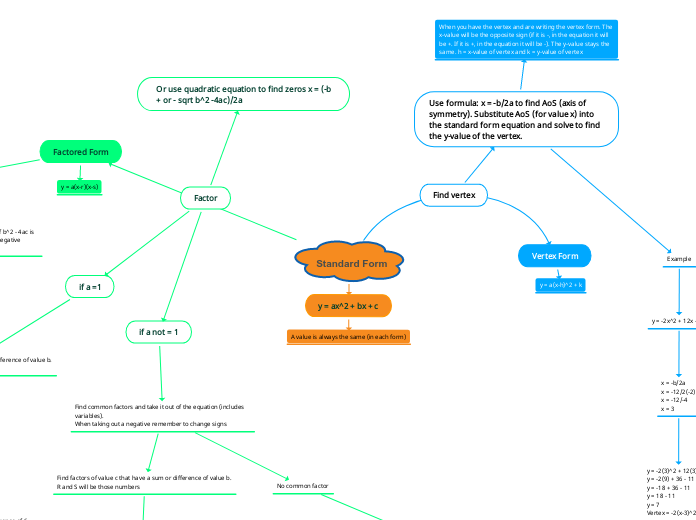
Factor

Or use quadratic equation to find zeros x = (-b + or - sqrt b^2 -4ac)/2a

if a =1

Find factors of value c that have a sum or difference of value b. R and s will be those two numbers

y = x^2 + 6x + 8

Find factors of 8 that have a sum or difference of 6

8 = 2x4

6 = 2+ 4

Therefore y = (x+2)(x+4)

a = 1

if a not = 1

Find common factors and take it out of the equation (includes variables). When taking out a negative remember to change signs

No common factor

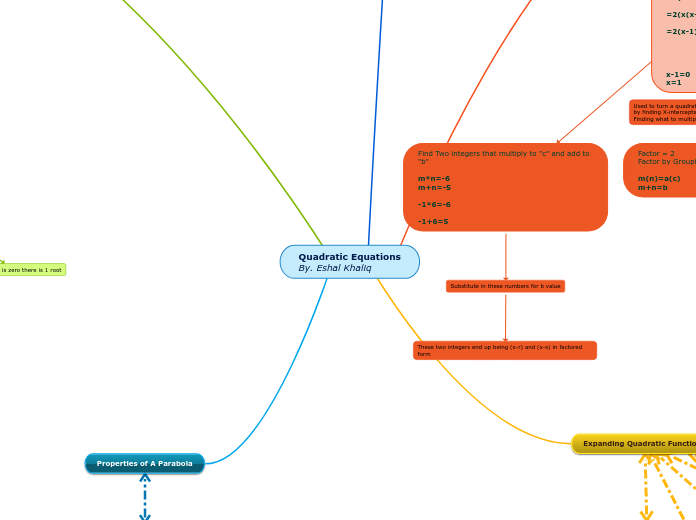
Multiply value a with value c. Find factors of the product that have a sum or difference of value b. With those 2 factors, replace value b. Common factor the 1st 2 terms then the last 2 terms.

y = 4x^2 + 7x + 3

4x3 = 12 7 = 3+4 y = 4x^2 + 3x + 4x + 3 y = x(4x + 3)+ 1(4x+3) therefore factored form is y = (x+1)(4x+3)

Find factors of value c that have a sum or difference of value b. R and S will be those numbers

y = -2x^2 + 14x - 24

Common factor of 2 (-2 so change signs)

y = -2(x^2 - 7x + 12)

Find factors of 12 that have a sum or difference of -7

12 = (-3)x(-4) -7 = -3-4 Therefore y = -2(x-3)(x-4)

Find vertex

Use formula: x = -b/2a to find AoS (axis of symmetry). Substitute AoS (for value x) into the standard form equation and solve to find the y-value of the vertex.

When you have the vertex and are writing the vertex form. The x-value will be the opposite sign (if it is -, in the equation it will be +. If it is +, in the equation it will be -). The y-value stays the same. h = x-value of vertex and k = y-value of vertex

Example

y = -2x^2 + 12x - 11

x = -b/2a x = -12/2(-2) x = -12/-4 x = 3

substitude AoS into equation for x to find y-value of vertex

y = -2(3)^2 + 12(3) - 11 y = -2(9) + 36 - 11 y = -18 + 36 - 11 y = 18 - 11 y = 7 Vertex = -2(x-3)^2 + 7

Standard Form

Vertex Form

y = a(x-h)^2 + k

y = ax^2 + bx + c

A value is always the same (in each form)

Factored Form

Special cases

When using the quadratic equation, if the result of b^2 - 4ac is negative, then there are no zeros (cannot sqrt a negative number!). This means there is no factored form.

y = a(x-r)(x-s)