La funzione
Link utili
Testi
Video
Esempi di funzione non matematica
Esempi di funzione matematica
Sottoargomento
Studio
Grafico
Studio concavità
Calcolo derivata seconda e ricerca dei punti di flesso
Natura punti stazionari
Max, min, flessi a tangente orizzontale
Calcolo derivata prima e ricerca punti stazionari
Casi particolari di funzioni non derivabili in punti appartenenti al dominio
Limiti agli estremi del dominio
Asintoti
DEFINIZIONE: È una retta a cui tende una funzione in un comportamento limite
obliquo
orizzontale
verticale
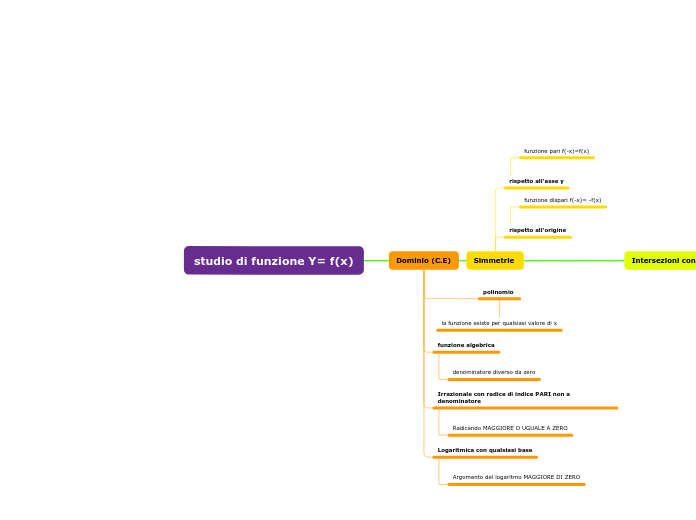
Intersezione con gli assi e studio del segno
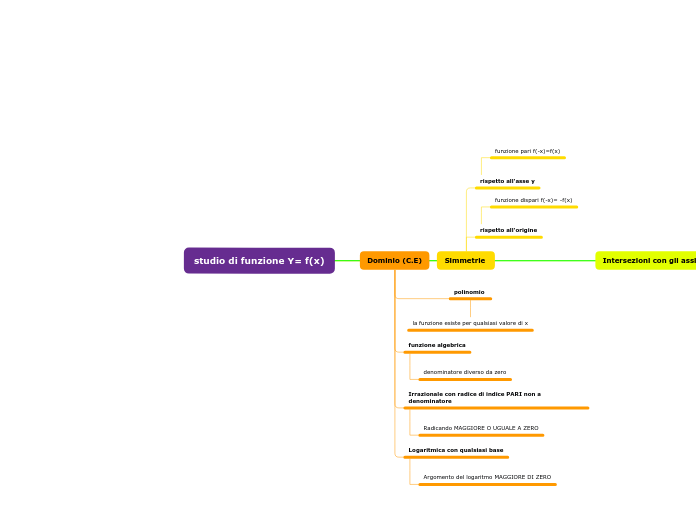
Simmetrie pari/dispari
Una funzione f(x) viene detta PARI quando per ogni x appartiene al dominio, cioè f(-x)=f(x) quindi ad esempio se noi calcoliamo la funzione in 4 essa deve dare lo stesso valore quando la calcoliamo in -4.
La loro caratteristica è quella di avere il grafico simmetrico rispetto all'asse delle ordinate.
La funzione f(x) è DISPARI se per ogni x appartenente al dominio vale la relazione f(-x)=-f(x) cioè se la funzione di 4 vale 7 allora quando la calcolerò in -4 dovrà valere -7, queste deve valere per ogni coppia di punti che si trovano in posizone simmetrica del dominio.
La loro caratteristica è quella di avere il grafico simmetrico rispetto all'origine.
Dominio
Cioè è l’insieme su cui la funzione è definita.
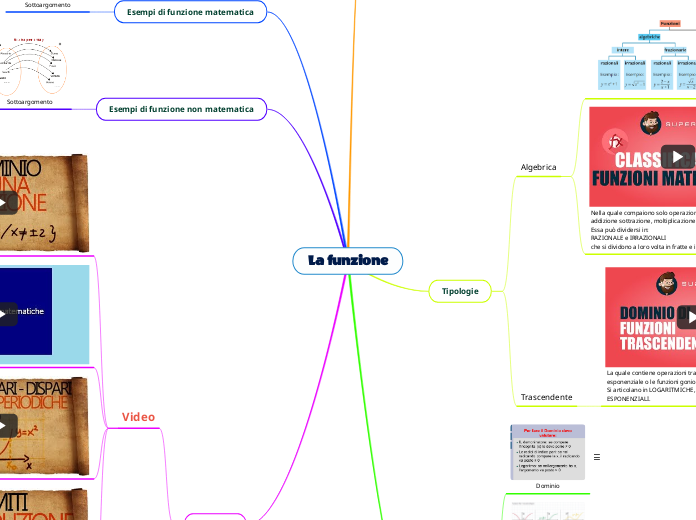
Tipologie
Trascendente
La quale contiene operazioni trascendenti: logaritmo, esponenziale o le funzioni goniometriche.
Si articolano in LOGARITMICHE, GONIOMETRICHE ed ESPONENZIALI.
Algebrica
Nella quale compaiono solo operazioni di tipo algebrico: addizione sottrazione, moltiplicazione, divisione, potenza.
Essa può dividersi in:
RAZIONALE e IRRAZIONALI
che si dividono a loro volta in fratte e intere.
Definizione
E' una relazione tra i due insiemi, A e B. La funzione dell'Insieme A e dell'insieme B è una funzione che ad ogni elemento di A associa uno e uno solo elemento di B.
OPPURE
Dati due insiemi X e Y, si dice funzione da X in Y una relazione che associa ad ogni elemento dell'insieme X, detto dominio, un unico elemento dell'insieme Y detto condominio.