Raymundo Pech
Análisis e interpretación de información
Es una actividad indispensable para generar
inferencias y tomar decisiones de forma más certera.
Análisis puntual
La atención al observar datos se centra en valores específicos o puntos
de un gráfico.
Análisis global
Permite reconocer tendencias en el comportamiento de los datos, a partir
de su análisis por intervalos o de la información como un todo.
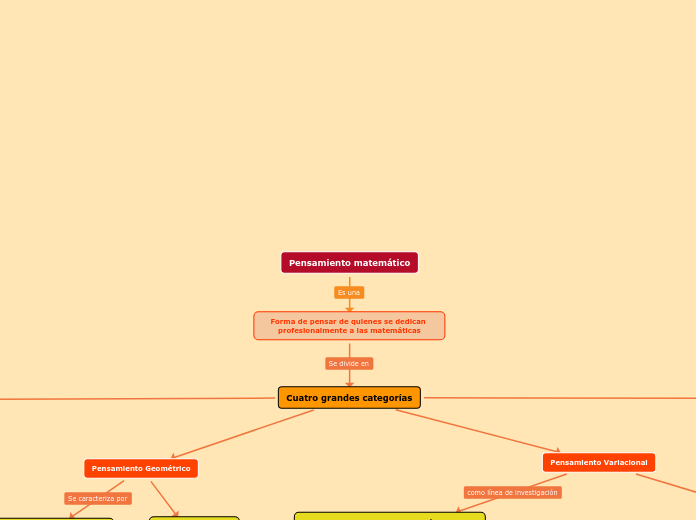
Pensamiento matemático
Forma de pensar de quienes se dedican profesionalmente a las matemáticas
Cuatro grandes categorías
Pensamiento Geométrico
Habilidades que se
desarrollan en el
pensamiento
geométrico
Dibujo y objeto
Se refiere a generar y
diferenciar entre
la representación de
un objeto del mismo objeto.
Validación
Se divide en
Demostración
Incorporar proposiciones
geométricas a una teoría
geométrica
Argumentación
Para validar afirmaciones
de lo que se esté trabajando
Construcción
Relación entre
propiedades
geométricas
Exploración
Resolver un problema
que da pie a la generación
de conjeturas
Visualización
En este se realizan asociaciones
de imágenes en la memoria
con otras imágenes mentales, las
cuales se relacionan considerando
propiedades.
Percepción
visual
Elementos que se perciben
a través del sentido de la vista
Relacionar figuras geométricas
con propiedades, transformaciones
traslaciones, así como elementos
espaciales
Pensamiento Estocástico
Pensamiento estadístico
Utiliza el concepto de que toda
actividad consiste en un conjunto de pasos interconectados que deben complementarse
y completarse para lograr una meta planteada.
Es una filosofía de pensamiento, no una forma de realizar
cálculos matemáticos.
Es la forma en que la información se ve, se procesa y se
convierte en pasos de acción.
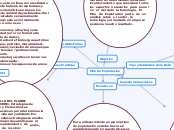
Pensamiento aletorio
experimentos y situaciones aleatorias
la irreversibilidad
La idea o noción de "Probabilidad"
Según Aristóteles hay tres tipos de nociones de probabilidad
El azar es divino y sobrenatural
El azar proviene de causas múltiples
El azar no existe y refleja nuestra ignorancia
Solo un razonamiento combinatorio, permite determinar el conjunto de posibilidades asociadas a un fenómeno aleatorio. En el cual, por su naturaleza no se puede asegurar que después de realizarlo, no es posible volver al estado inicial.
el pensamiento determinista
Pensamiento Variacional
Lo constituyen estructuras y habilidades cognitivas que se requieren para explicar los fenómenos de variación y cambio.
Prácticas Sociales
Son aquellas prácticas humanas que posibilitan la construcción del conocimiento matemático, en los usos y quehacer de una comunidad para dar solución a un problema en un contexto específico.
Prácticas asociadas al pensamiento variacional
Aproximar
Acumular
Comparar
Optimizar
Predecir
Lenguaje variacional
Describir qué cambia,
cómo y cuánto cambia aquello que cambia en una situación.
Estructuras variacionales
Un conjunto de arreglos qué seguir para resolver un problema.
El resultado de actividades y acciones que permiten desarrollar en el estudiante
herramientas para seguir un cierto camino en la resolución de una situación variacional.
Su objeto de estudio son los fenómenos de enseñanza, aprendizaje y comunicación de los saberes matemáticos propios de la variación y el cambio
variación y cambio
Relaciones entre variables
Escalonada
Acelerada
Inversa
Periódica
Polinomial
Directamente proporcional
lineales
La variación se entiende como una cuantificación del cambio.
El cambio denota la modificación de estado, apariencia, comportamiento o condición de un objeto, cuerpo, o sistema
Lenguaje y pensamiento algebraico
Modos de pensamiento
algebraico
Modelar
Generalizar
Tres fases
1. Regularidad, diferencia
y relación entre partes
2. Descripción o
exposición verbal
3. Escritura
Simbolizar
Expresar mediante símbolos
regularidades matemáticas.
Tres Fases
3. Interpretación del
resultado matemático
2. Solución o análisis
del problema
1. Formulación de un
problema real en
términos matemáticos
Invertir y deshacer
operaciones
Habilidad cognitiva para
realizar operaciones,
establecer relaciones entre
variables.
Lenguaje algebraico
Tres categorías
Pragmática
El sentido que se da al discurso
matemático en función del
contexto en que se enuncia.
Semántica
Es el sentido de los
objetos y expresiones
algebraicas.
Sintaxis
La relación entre signos y
símbolos, haciendo énfasis
en el orden.