Floating topic
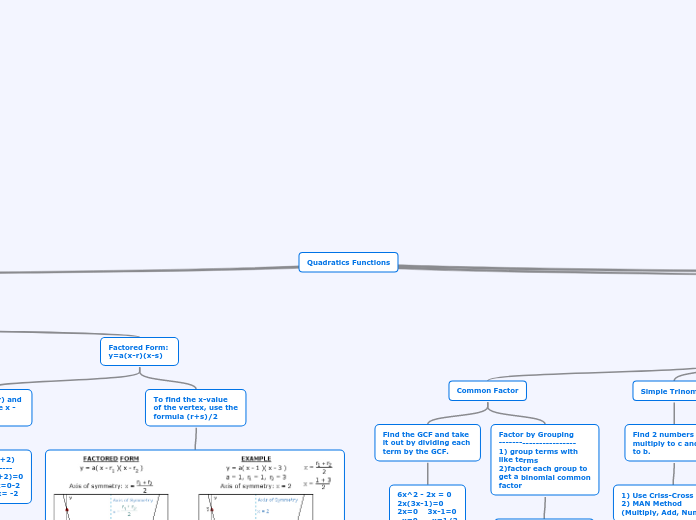
X-intercept /Factored Form
The axis of symmetry
is a vertical line that
separates the parabola into
two congruent halves.
Optimal value
The optimal value
represents the
y-coordinate
The Axis of symmetry
By using the QUADRATIC FORMULA
Completing
the square
refers to
factoring a
perfect square
trinomial to get
the square
of a binomial
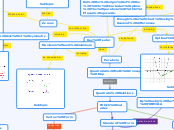
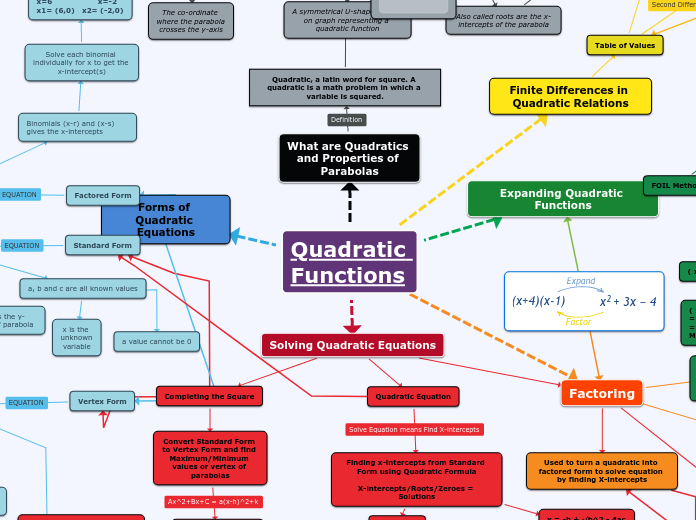
Quadratics Math Concept Map
Parabola
y = x²
y = x² points to the coordinates
(0,0), which is the origin of the
Cartesian plane. The parabola
faces upwards.
through a chart using second differences
Second differences, can assists with figuring our whether there is a linear relation, a quadratic relation, or neither.
Key features
Maximum and minimum
Zeroes
Zeros are
where a
parabola
cross the
x-axis. A
parabola
may have
one,two,
or no
zeros
Subtopic
Quadratic Relations
Which includes
X-intercept/Factored Form
y = a(x-p)(x-q)
can also be changed into Standard form
Standard Form
y = ax² + bx + c
complete the
square if a ≠1
y = 2x² - 16x -1
y = (2x² - 16x) - 1
y = 2(x² - 8x) - 1
y = 2(x²- 8x + 16 - 16) - 1
y = 2(x² - 8x + 16) - 16(2) - 1
y = 2(x - 4)² - 33
The first blue Line, is the standard form when a ≠1. Group the x-terms as shown in the red line. Common factor just the a-value from the x-terms. Divide the coefficient of the middle term by 2, square it,
then add and subtract that number inside the brackets. Remove the subtracted term from the brackets. Multiply it by the "a" value you factored out. Factor the brackets as a perfect square trinomial.
complete the square if a=1
y = x² - 6x +4
y = (x² - 6x) +4
y = (x² - 6x + 9 - 9) +4
y = (x²- 6x + 9) - 9 + 4
y = (x-3)² - 5
The first blue Line is the standard form.The next line shows how the x variables are grouped. After grouping the x variables divide the middle coefficient by two, square the result, than add and subtract the number inside the brackets.Remove the subtracted term, from the brackets.Factor the brackets as a perfect square trinomial. Remember to solve whats outside the brackets as well. This is the result of factoring the standard form, which is now the vertex form.
Vertex Form
y = a(x-h)² + k
a-value
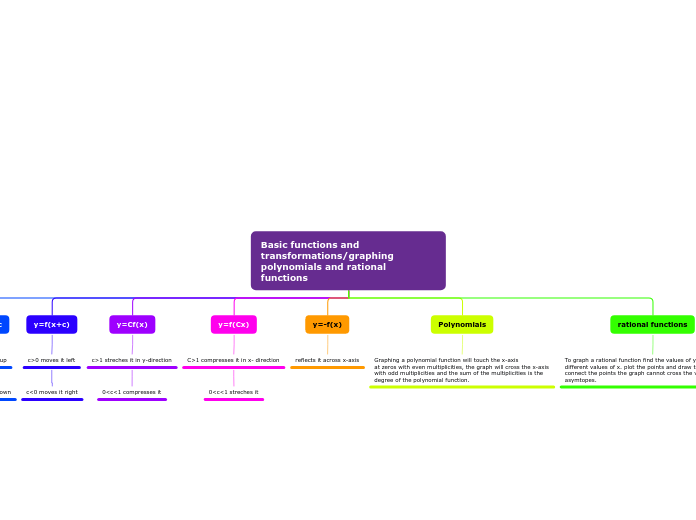
Transformations
The parabola is stretched
More specific on how much the parabola is being compressed or stretched, use the equation, "1a,3a,5a". Substitute the a-values into the equation, as shown below.
The parabola is compressed
The parabola will face upwards
The parabola will face downwards
Translations, which can be either
y = a(x-h)² + k , the k-value is the horizontal translation
y = a(x-h)² + k , the h-value is the vertical translation
The VERTEX(h,k)