作者：Angelo Mustone 1 年以前
60
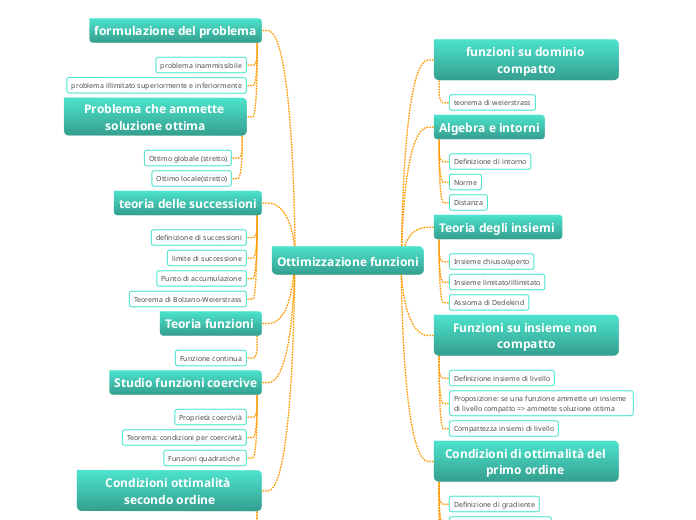
Ottimizzazione funzioni
Il testo tratta vari argomenti fondamentali in matematica, concentrandosi soprattutto sull'ottimizzazione delle funzioni. Viene esplorata la teoria delle funzioni attraverso concetti come la continuità, le derivate direzionali e la definizione di gradiente.
開啟
Ottimizzazione funzioni
Condizioni ottimalità secondo ordine Teorema della media del secondo ordine Matrice Hessiana Studio funzioni coercive Funzioni quadratiche Teorema: condizioni per coercività Proprietà coercivià Teoria funzioni Funzione continua teoria delle successioni Teorema di Bolzano-Weierstrass Punto di accumulazione limite di successione definizione di successioni formulazione del problema Problema che ammette soluzione ottima Ottimo locale(stretto) Ottimo globale (stretto) problema illimitato superiormente e inferiormente problema inammissibile Condizioni di ottimalità del primo ordine Derivate direzionali Approssimazione di una funzione al primo ordine in un punto Condizione differenziabilità Definizione di gradiente Funzioni su insieme non compatto Compattezza insiemi di livello Proposizione: se una funzione ammette un insieme di livello compatto => ammette soluzione ottima Definizione insieme di livello Teoria degli insiemi Assioma di Dedekind Insieme limitato/illimitato Insieme chiuso/aperto Algebra e intorni Distanza Norme Definizione di intorno funzioni su dominio compatto teorema di weierstrass
